- The integer (Obviously!)
- A perfect square that can be got from the integer
- The remainder in subtracting the perfect square from the integer
As an example, let's find the square root of the integer 7:
PS: You will notice (after a number of practices) that the values got using this method differ slightly from the ones got from the calculator. Do not be alarmed, the values are still correct nonetheless.
I do hope this is helpful and would come in handy when we need it.
Please let me know what your thoughts on any other trick you know.
Waiting for your comments. ;-)

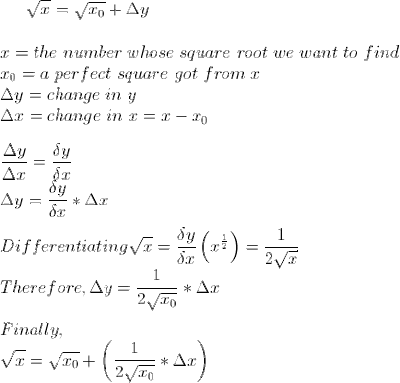

Brilliant! Never seen this before. Thanks for sharing...
ReplyDeleteThanks. I hope it comes in handy...
DeleteI don't know calculus but it appears you're talking about something like this?
ReplyDeletehttp://www.quora.com/Mathematics/How-can-I-find-the-square-root-of-22-without-a-calculator/answer/Mark-Eichenlaub
Yes Komla. Same idea, different approaches. ;-)
DeleteManual square root analogous to long division:
ReplyDeletehttps://docs.google.com/drawings/d/19FAnd5R9P3SWA7ZanWrjNPEgkwRsMU-WBBX9Lwm9ulg/pub?w=960&h=720
Better link:
Deletehttps://docs.google.com/drawings/d/19FAnd5R9P3SWA7ZanWrjNPEgkwRsMU-WBBX9Lwm9ulg/pub?w=1440&h=1080
and am I the only person to remember this method?
Another approach, without calculus, but that is basically the same is this:
ReplyDelete0) looking for sqrt(X) = Y => X = Y^2
1) nearest integral square: X0 = Y0^2
1.1) Y0 may be greater or less than, i.e. next integer up or down from, Y
2) deltaY = Y - Y0; Y = Y0 + deltaY
3) deltaX = X - X0
4) Y^2 = (Y0 + deltaY)^2 = Y0^2 + 2 Y0 deltaY + deltaY^2
5) approximation: drop deltaY^2; less than 1/4 if Y0 is closest integer to Y
5.1) this is the same as the [deltaY/deltaX = dy/dx (partial)] in the post above
6) Y^2 ~ Y0^2 + 2 Y0 deltaY
7) solve for deltaY:
7.1) deltaY ~ (Y^2 - Y0^2) / (2 Y0)
7.2) deltaY ~ (X - X0) / (2 Y0)
7.2) deltaY ~ deltaX / (2 sqrt(X0)) QED
8) Finally, error in Y calculated by this
method, assuming deltaY < 1/2, will be
less than 1/(8 X0)